Democratic elections permit us to vote for whomever we perceive has the highest expectation to do better with the issues we care about. Let’s simplify and assume we can quantify how satisfied we are with an elected official’s performance. Denote this quantity with X. Because when we cast our vote we still don’t know for sure how the candidate will perform, we base our decision on what we expect, denoted here with E(X). Thus we try to maximize E(X). However, both political theory and data tell us that in US presidential elections only two parties have a non-negligible probability of winning. This implies that E(X) is 0 for some candidates no matter how large X could potentially be. So what we are really doing is deciding if E(X-Y) is positive or negative with X representing one candidate and Y the other.
In past elections some progressives have argued that the difference between candidates is negligible and have therefore supported the Green Party ticket. The 2000 election is a notable example. The 2000 election was won by George W. Bush by just five electoral votes. In Florida, which had 25 electoral votes, Bush beat Al Gore by just 537 votes. Green Party candidate Ralph Nader obtained 97,488 votes. Many progressive voters were OK with this outcome because they perceived E(X-Y) to be practically 0.
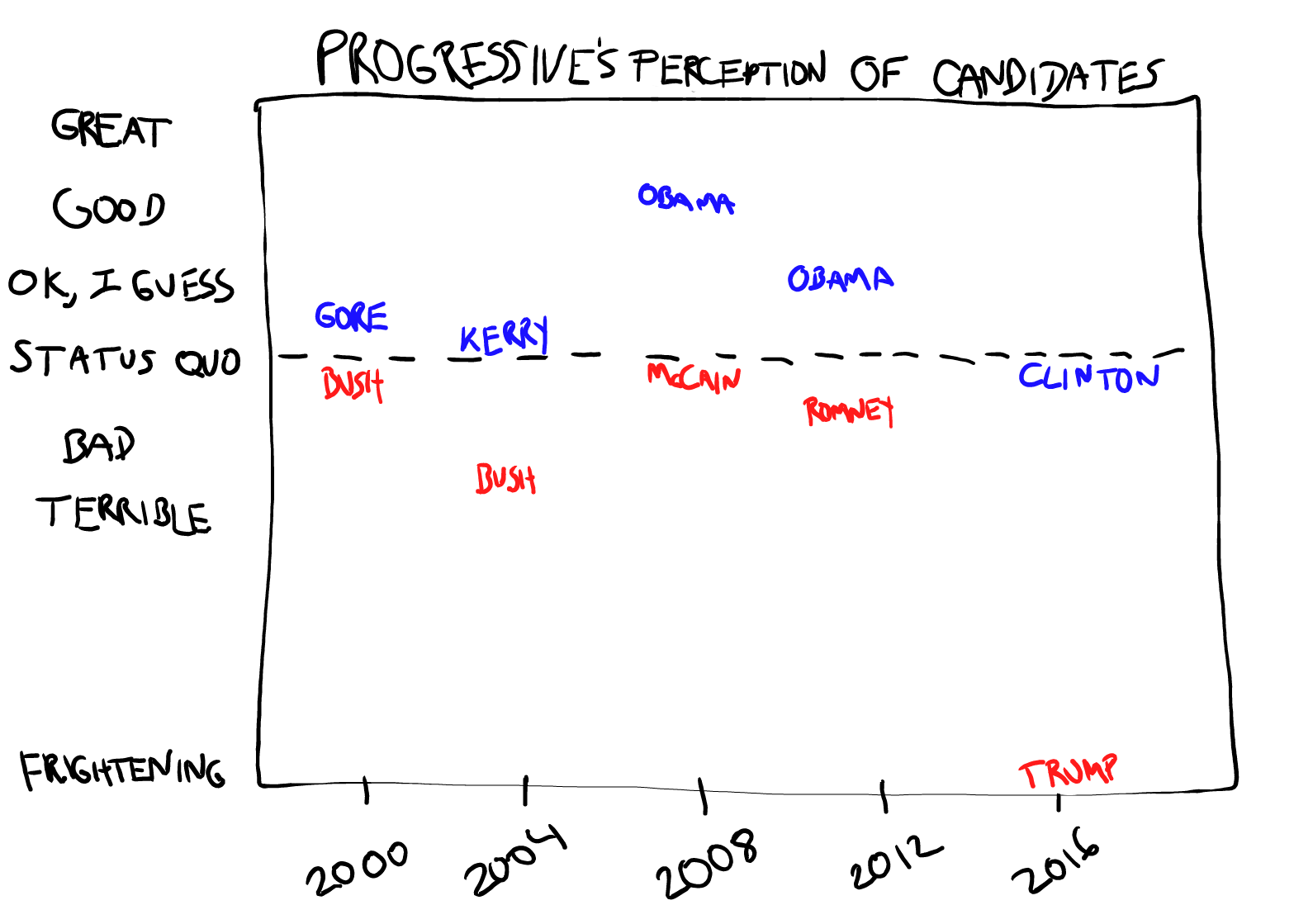
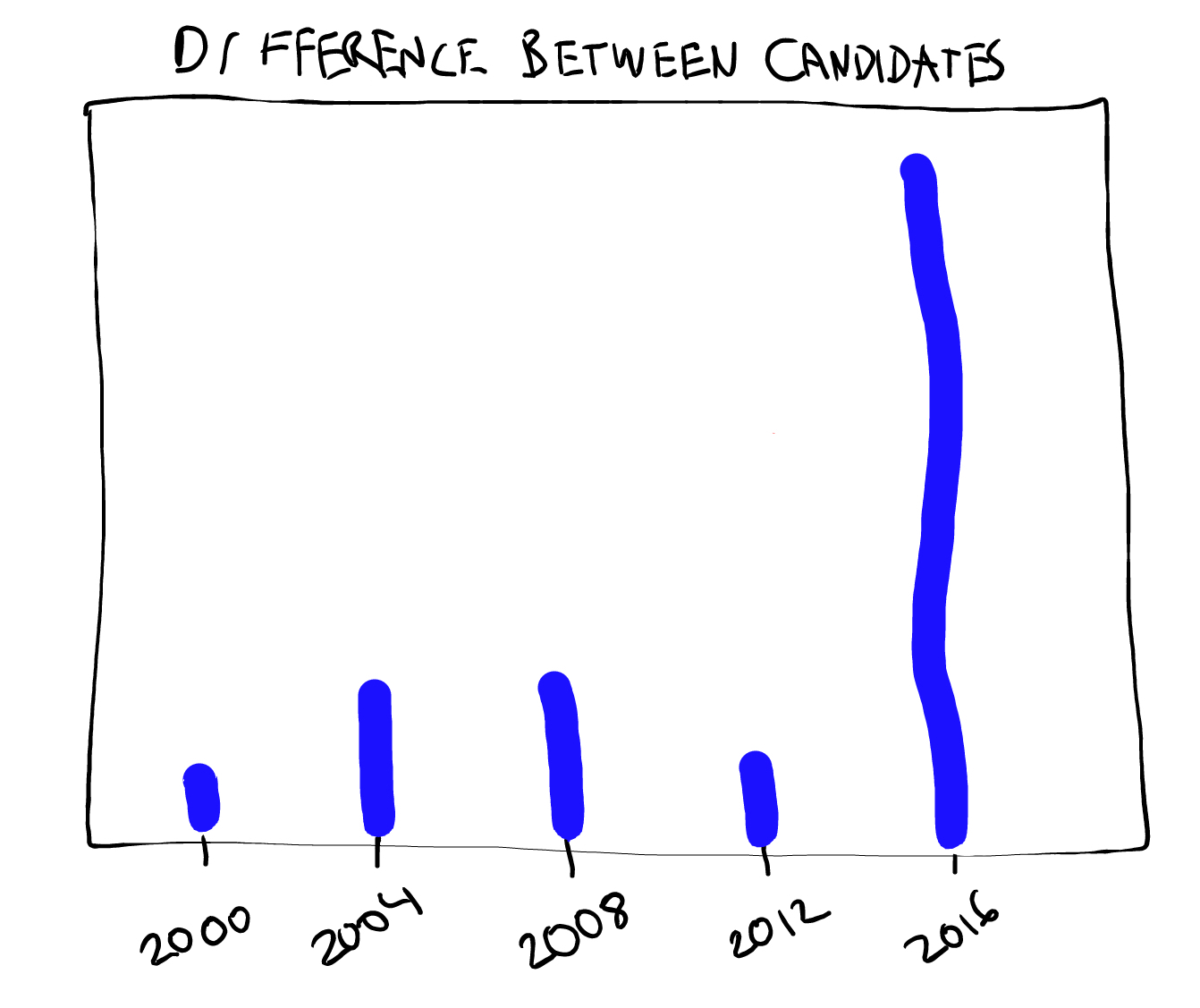
In contrast, in 2016, I suspect few progressives think that E(X-Y) is anywhere near 0. In the figures below I attempt to quantify the progressive’s pre-election perception of consequences for the last five contests. The first figure shows E(X) and E(Y) and the second shows E(X-Y). Note despite E(X) being the lowest in the last past five elections, E(X-Y) is by far the largest. So if these figures accurately depict your perception and you think like a statistician, it becomes clear that this is not the election to vote third party.